Da click al grupo que te corresponda:
Sucesiones y series (aritméticas y geométricas) de números, bosquejando funciones discretas (lineales y exponenciales).
Sucesiones y series numéricas particulares
¿Qué es una sucesión?
Una sucesión es un conjunto de cosas (normalmente números) en un cierto orden.
 |
Finita o infinita
Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita
En orden
Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!
Como un conjunto
Una sucesión es muy parecida a un conjunto, pero:
- los términos están en orden (en los conjuntos el orden no importa).
- el mismo valor puede aparecer muchas veces (en los conjuntos solo una vez).
Notación
| Las secuencias también usan la misma notación que los conjuntos: se enumera cada elemento, separados por una coma, y luego se ponen llaves alrededor de todo. | {3, 5, 7, ...} |
Los corchetes { } también se conocen como "llaves".
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
 |
|
Entonces podemos escribir una regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
¿Puedes calcular el 50º término? ¿Y el 500º?
Aquí está otro ejemplo:
La regla
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
¡Pero la regla debería ser una fórmula!
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:
- 10º término,
- 100º término, o
- n-ésimo término (donde n puede ser cualquier número positivo que queramos).
Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).
Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n | Término | Prueba |
|---|---|---|
| 1 | 3 | 2n = 2×1 = 2 |
| 2 | 5 | 2n = 2×2 = 4 |
| 3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
| n | Término | Regla |
|---|---|---|
| 1 | 3 | 2n+1 = 2×1 + 1 = 3 |
| 2 | 5 | 2n+1 = 2×2 + 1 = 5 |
| 3 | 7 | 2n+1 = 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
2n+1
Pero las matemáticas son tan poderosas que podemos encontrar más de una regla que funcione para cualquier sucesión.
Por lo tanto, es mejor decir "Una regla" en lugar de "La regla" (a menos que sepamos que es la regla correcta).
Para encontrar un número que falta en una sucesión, primero tienes que conocer la regla
Sucesiones Triangular
Sucesiones cuadráticas
 Para ilustrar lo anterior, veamos el siguiente ejemplo: Tenemos la sucesión 2, 6, 12, 20, 30 si calculamos las primeras diferencias obtenemos:6-2 = 4 ; 12 -6= 6 ; 20-12=8; 30-20=10 sus diferencias no son constantes, es decir no se repite la misma cantidad en todas sus diferencias, entonces este seria el primer nivel. Para el segundo nivel volvemos hacer las diferencias ahora del primer nivel: 4 , 6, 8, 10 obteniendo: 6-4=2; 8 -6=2; 10-8= 2 . Ahora si hay una constante que es 2. Por lo tanto la sucesión es cuadrática.
Si queremos encontrar su regla utilizamos el siguiente procedimiento:
PASO 1: Calculamos las diferencias del 1er. nivel y del 2° nivel, para nuestro ejemplo ya las tenemos.
Para ilustrar lo anterior, veamos el siguiente ejemplo: Tenemos la sucesión 2, 6, 12, 20, 30 si calculamos las primeras diferencias obtenemos:6-2 = 4 ; 12 -6= 6 ; 20-12=8; 30-20=10 sus diferencias no son constantes, es decir no se repite la misma cantidad en todas sus diferencias, entonces este seria el primer nivel. Para el segundo nivel volvemos hacer las diferencias ahora del primer nivel: 4 , 6, 8, 10 obteniendo: 6-4=2; 8 -6=2; 10-8= 2 . Ahora si hay una constante que es 2. Por lo tanto la sucesión es cuadrática.
Si queremos encontrar su regla utilizamos el siguiente procedimiento:
PASO 1: Calculamos las diferencias del 1er. nivel y del 2° nivel, para nuestro ejemplo ya las tenemos. PASO 2: Utilizamos la expresión 2a para calcular el valor de a, esta expresión se iguala al valor obtenido para el 1er, término del segundo nivel de diferencias.
PASO 2: Utilizamos la expresión 2a para calcular el valor de a, esta expresión se iguala al valor obtenido para el 1er, término del segundo nivel de diferencias.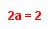 resolvemos la ecuacióna= 2/2a= 1
PASO 3: Utilizamos la expresión 3a + b para calcular el valor de b y sustituimos el valor obtenido para a. Esta expresión se iguala con el 1er, término del primer nivel de diferencias.
resolvemos la ecuacióna= 2/2a= 1
PASO 3: Utilizamos la expresión 3a + b para calcular el valor de b y sustituimos el valor obtenido para a. Esta expresión se iguala con el 1er, término del primer nivel de diferencias.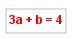 sustituimos a=1(3)(1) + b = 4multiplicamos3 + b = 4despejamos bb= 4 -3b= 1
PASO 4: Utilizamos la expresión a +b+ c para calcular el valor de c y sustituimos los valores obtenidos para a y b. Esta expresión se iguala con el 1er, término de la sucesión.a +b + c = 2sustituimos a=1 ; b=1 y despejamos c1 + 1 +c = 22 + c = 2c= 2 – 2c= 0
PASO 4:Sustituimos los valores encontrados para a, b y c en la fórmula de la regla.
sustituimos a=1(3)(1) + b = 4multiplicamos3 + b = 4despejamos bb= 4 -3b= 1
PASO 4: Utilizamos la expresión a +b+ c para calcular el valor de c y sustituimos los valores obtenidos para a y b. Esta expresión se iguala con el 1er, término de la sucesión.a +b + c = 2sustituimos a=1 ; b=1 y despejamos c1 + 1 +c = 22 + c = 2c= 2 – 2c= 0
PASO 4:Sustituimos los valores encontrados para a, b y c en la fórmula de la regla. esta es la regla para la sucesión.
PASO 5: Comprobamos la regla para los dos primeros términos.
esta es la regla para la sucesión.
PASO 5: Comprobamos la regla para los dos primeros términos.


En una sucesión aritmética, la diferencia entre un término y el siguiente es una constante.
En otras palabras, simplemente sumamos el mismo valor cada vez ... infinitamente.
En general, podríamos escribir una sucesión aritmética así:
{a, a+d, a+2d, a+3d, ... }
donde:
- a es el primer término, y
- d es la diferencia entre los términos (llamada "diferencia común")
Regla
Podemos escribir una sucesión aritmética como regla:
xn = a + d(n−1)
(Usamos "n−1" porque la d no se usa en el 1er término).
Las sucesiones aritméticas a veces se llaman progresiones aritméticas.
Tema avanzado: Sumar una serie aritmética
Para sumar los términos de esta sucesión aritmética:
a + (a+d) + (a+2d) + (a+3d) + ...
usa esta fórmula:
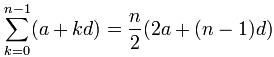
¿Cuál es ese símbolo raro? Se llama Notación Sigma
| (llamado Sigma) significa "suma" |
Y abajo y arriba se muestran los valores iniciales y finales:
Dice "Suma n donde n va de 1 a 4. Respuesta=10
Aquí está cómo usarlo:
Nota al pie: ¿Por qué funciona la fórmula?
Veamos porqué funciona la fórmula, pues podremos usar un "truco" interesante que vale la pena conocer.
Primero, llamaremos a toda la suma "S":
Luego, reescribimos S en orden inverso:
Ahora sumamos esas dos, término por término:
| S | = | a | + | (a+d) | + | ... | + | (a + (n-2)d) | + | (a + (n-1)d) |
| S | = | (a + (n-1)d) | + | (a + (n-2)d) | + | ... | + | (a + d) | + | a |
| 2S | = | (2a + (n-1)d) | + | (2a + (n-1)d) | + | ... | + | (2a + (n-1)d) | + | (2a + (n-1)d) |
¡Cada término es igual! Y hay "n" de ellos, así que ...
Ahora, tan solo dividimos entre 2 y obtenemos:
S = (n/2) × (2a + (n−1)d)
Que es nuestra fórmula:
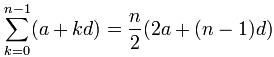
Sucesiones geométricas
En una sucesión geométrica, cada término se encuentra multiplicando el término anterior por una constante.
Ejemplo:
En general, escribimos una sucesión geométrica como esta:
{a, ar, ar2, ar3, ... }
donde:
- a es el primer término y
- r es el factor entre los términos (llamado "cociente común"o "razón")
Ejemplo: {1,2,4,8,...}
Pero ten cuidado, r no debe ser 0:
- Cuando r=0, obtenemos la sucesión {a, 0,0, ...}, la cual no es geométrica
La regla
También podemos calcular cualquier término usando la regla:
xn = ar(n-1)
(Se utiliza "n-1" porque ar0 representa al primer término)
Ejemplo:
Una sucesión geométrica también puede tener valores cada vez más pequeños:
Ejemplo:
¿Por qué se llama sucesión "geométrica"?
Porque es como aumentar las dimensiones en geometría:
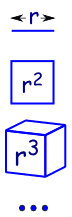 | una línea es unidimensional y tiene una longitud de r |
| en 2 dimensiones un cuadrado tiene un área de r2 | |
| en 3 dimensiones un cubo tiene volumen r3 | |
| etc (sí, podemos tener 4 y más dimensiones en matemáticas). |
Las sucesiones geométricas a veces se llaman progresiones geométricas.
Sumando una sucesión geométrica
Para sumar esto:
a + ar + ar2 + ... + ar(n-1)
(Cada término es ark, donde k comienza en 0 y sube hasta n-1)
Podemos usar esta práctica fórmula:
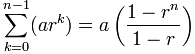
a es el primer término
r es la "razón" entre términos
n es el número de términos
¿Cuál es ese símbolo raro? Se llama Notación Sigma
| (llamado Sigma) significa "suma" |
Y abajo y arriba se muestran los valores iniciales y finales:
Dice "Suma n donde n va de 1 a 4. Respuesta=10
La fórmula es fácil de usar ... simplemente "pon" los valores de a, r y n
Ejemplo: Suma los primeros 4 términos de
Usando la fórmula
Veamos la fórmula en acción:
Ejemplo: granos de arroz en un tablero de ajedrez
Y otro ejemplo, esta vez con r menor que 1:
Ejemplo: Suma los primeros 10 términos de la sucesión geométrica que se reduce a la mitad cada vez:
{ 1/2, 1/4, 1/8, 1/16, ... }
¿Por qué funciona la fórmula?
Veamos porqué funciona la fórmula, pues podremos usar un "truco" interesante que vale la pena conocer.
¿Te das cuenta que S y S·r son similares?
¡Ahora réstalos!
¡Guauu! Todos los términos en el medio se cancelan perfectamente.
(Lo cual es un buen truco)
Entonces, si restamos S·r de S obtenemos un resultado simple:
S − S·r = a − arn
Vamos a reorganizarlo para encontrar S:
Que es nuestra fórmula (¡ta-da!):
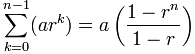
Infinite Geometric Series
¿Qué ocurre cuando n va hasta infinito?
Podemos usar esta fórmula:
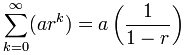
Pero sé cuidadoso:
r debe estar entre (pero sin incluir) −1 y 1
y r no debería ser 0 porque la sucesión {a, 0,0, ...} no es geométrica
Volvamos a nuestro ejemplo anterior y veamos qué sucede:
Ejemplo: Suma TODOS los términos de la sucesión geométrica que se reduce a la mitad cada vez:
{ 12, 14, 18, 116, ... }
¿No me crees? Solo mira este cuadrado: Sumando 12 + 14 + 18 + ... ¡Logramos abarcarlo todo! |  |
Decimal recurrente
En otro artículo preguntamos "¿Es verdad que 0,999... es igual a 1?", bueno, veamos si podemos calcularlo:
Ejemplo: Calcula 0,999...
Así que ahí lo tenemos ... Las sucesiones geométricas (y sus sumas) pueden hacer todo tipo de cosas asombrosas y poderosas.
Números triangulares
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
La Sucesión Triangular se genera a partir de una pauta de puntos en un triángulo.
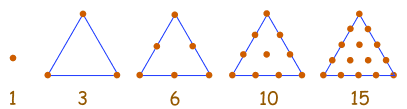
Añadiendo otra fila de puntos y contando el total encontramos el siguiente número de la sucesión.
Pero es más fácil usar la regla:
xn = n(n+1)/2
Números cuadrados
| 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
El siguiente número se calcula elevando al cuadrado su posición en la sucesión.
La regla es xn = n2
Series y sumas parciales
¿Qué es una serie numérica?
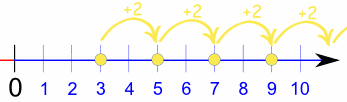
Una serie numérica es una secuencia de números ordenados, llamados términos, entre los cuales hay una relación que hay que descubrir, para completar la serie.
Por ejemplo, en la serie 0 - 7 - 14 - 21 existe una relación: el número 7. Esto quiere decir que para seguir la secuencia, solo debemos sumar el número 7 al último valor presentado, el 21.

Aquí podrás ver más ejemplos:
- 5 - 10 - 15 - 20 - 25 - 30. La relación va de 5 en 5
- 10 - 20 - 30 - 40 - 50. La relación va de 10 en 10
- 15 - 12 - 9 - 6 - 3 - 0. La relación va de 3 en 3, pero en este caso de mayor a menor
Ahora que ya conoces las sucesiones, el siguiente tema por aprender es cómo sumarlas.
Cuando sumamos solo una parte de la sucesión decimos que hacemos una suma parcial.
Pero una suma de una sucesión infinita se llama "serie" (parece como si fuera otro nombre para las sucesiones, pero en realidad es una suma). Lee Series Infinitas.









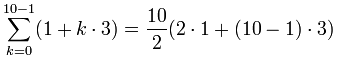

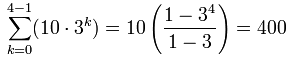
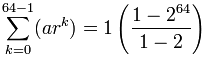
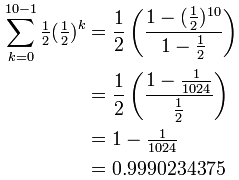

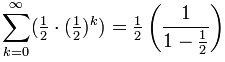
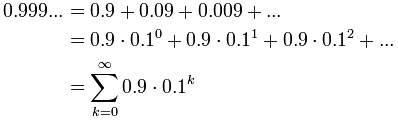
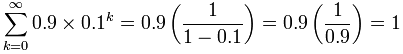


disculpe profe, ¿tendremos que tocar todos los temas que tiene este blog en nuestro powerpoint?
ResponderEliminar