CURSO PROPEDÉUTICO: Sesión 04

 

CURSO PROPEDÉUTICO

Link de clases virtuales:

Da click al grupo que te corresponda:

1AM 

1BM 

1CM 

1 DM 

Aplica la proporcionalidad directa e inversa en la solución de problemas vinculados con su vida cotidiana.

Proporción Directa

Qué es la proporcionalidad directa y para qué sirve.

Antes necesitamos saber qué es una magnitud. Una magnitud es aquello que se puede medir. Por ejemplo, el peso de una persona, el número de albañiles trabajando, el número de plátanos, la cantidad de pienso que come un perro, la distancia entre dos pueblos o la velocidad de un caballo al galopar.

Todas estas magnitudes se pueden relacionar con otras.

Se puede relacionar:

• El peso de una persona con la talla de ropa que usa.
• El número de albañiles trabajando con el tiempo que tardan en terminar la obra.
• El número de plátanos con el número de cajas necesarias para colocarlos.
• La distancia entre dos pueblos con el tiempo que se tarda en ir de uno a otro.
• La velocidad de un caballo galopando con el tiempo que tarda el caballo en llegar de un punto a otro.

Hay varios tipos de relaciones. Hoy veremos solo una de ellas: la proporcionalidad directa

Para que dos magnitudes mantengan una relación de proporcionalidad directa tienen que estar relacionadas de tal forma que si duplicamos una, la otra se tiene que duplicar, si la triplicamos la otra también y si la reducimos a la mitad la otra también se tiene que reducir. Se puede entender que si aumentamos la cantidad de una, la otra tiene que aumentar también proporcionalmente.

¿Qué relación podemos ver entre el número de plátanos y el número de cajas que necesitamos para guardarlos?

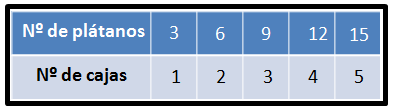
Podréis observar que cuantos más plátanos tenemos más cajas necesitamos, ¿verdad? Estas dos magnitudes mantienen una relación proporcionalmente directa.

Es importante saber que el cociente (razón o proporción) entre dos magnitudes directamente proporcionales es siempre constante. En nuestro ejemplo tenemos que la razón es 3.

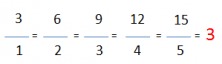
Las relaciones de proporcionalidad aparecen con mucha frecuencia en nuestra vida cotidiana.

¿Alguna vez habéis comprado caramelos? ¿Cómo calculabais la cantidad de dinero que teníais que pagar por los caramelos?

¿Qué me podéis decir de estas dos magnitudes, el número de cerdos y el número de fardos de paja que se necesita para alimentarlos?

¿Podríais decir que mantienen una proporcionalidad directa?

Si quieres aprender a resolver problemas de proporcionalidad, revisa este post de problemas de proporcionalidad, tienes varios ejemplos para practicar.

Proporción Inversa

Para empezar debemos recordar que una magnitud es todo aquello que se puede medir.

Si no te acuerdas bien, revisa este post anterior en el que hablábamos de la proporcionalidad directa y se explica el concepto de magnitud.

Muchas magnitudes están relacionadas con otras, como por ejemplo:

• Cantidad de juguetes que tengas con el espacio que ocupan.
• La velocidad a la que va un coche con el tiempo que tarda en recorrer un trayecto.
• El tamaño de tu habitación con el tiempo que tardas en limpiarla.
• El tiempo que pasa un alimento en un horno encendido con lo que tarda en cocinarse.
• Lo que tarda en llenarse una piscina en relación al caudal del agua.

Ya vimos en la entrada de proporcionalidad directa que hay relaciones en las que cuanto más crece una de las magnitudes más crece la otra. Pero cuando una magnitud crece y la otra disminuye proporcionalmente, se le llama proporcionalidad Inversa.

Dos magnitudes son inversamente proporcionales si al multiplicar (o dividir) una de ellas por un número, la otra queda dividida (o multiplicada) por el mismo número.

Cuanto mayor velocidad lleve el coche de carreras

menos tiempo tardará  en dar una vuelta al circuito

Imaginemos que dando una vuelta al circuito a 100 km/h, el coche tarda 12 min. En este caso y sabiendo que existe una relación de proporcionalidad inversa podremos decir que si multiplicamos la velocidad por 2 (200 km/h), entonces el tiempo por vuelta quedará dividido entre 2 (6 min).

Si por el contrario, redujera su velocidad a la mitad (100 km/h : 2 = 50 km/h) el tiempo por vuelta sería al doble (12 min x 2 = 24 min)

Si el coche diera su última vuelta en 4 min, ¿qué habría pasado con la velocidad del coche durante esa vuelta?

(12 min : 4 min = 3)  Como el tiempo se ha dividido entre 3, la velocidad se tiene que multiplicar por 3  (3 x 100 km/h = 300 km/h). Es decir que la velocidad a la que el coche dio su última vuelta fue 300 km/h.

Con estos ejemplos podemos observar el porqué del nombre INVERSA para este tipo de relación de proporcionalidad. Lo que ocurre con una de las magnitudes ocurre de forma INVERSA con la otra magnitud, cuando una crece la otra disminuye y viceversa.

Ahora, igual que ocurre con la proporcionalidad directa, vamos a hallar la Razón de Proporción.

Para calcular la razón tenemos que multiplicar las cantidades de cada magnitud relacionadas entre sí.

• 100 km/h x 12 min = 1200
• 200 km/h x 6 min = 1200
• 50 km/h x 24 min = 1200
• 300 km/h x 4 min = 1200

Al ver esto recordamos que la razón de proporción es una constate, es decir que es igual para cada par de números que representan las magnitudes relacionadas. En este caso la razón de proporción es 1200

Si quieres en esta entrada puedes aprender a resolver problemas de proporcionalidad.

Porcentaje

Si hablamos de porcentajes a todos nos resulta un tema familiar, pero: ¿sabríamos decir qué es un porcentaje? ¿cómo se calcula? y ¿qué significa exactamente? Este post va a resolver todas estas dudas, ¡vamos a por él!

El porcentaje es, realmente, un símbolo.

Un símbolo que representa una fracción de denominador 100. Así, en el lenguaje escrito, es mucho más sencillo escribir el porcentaje que la fracción:

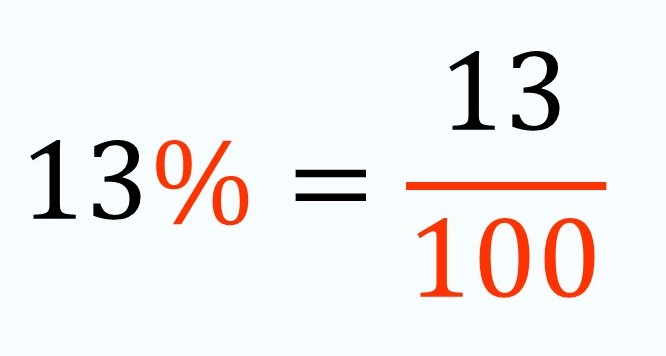
Este símbolo (%) se lee como “por ciento” e indica, como hemos dicho, el número de partes en que la unidad, o cantidad de referencia, ha sido dividida. Es decir, el porcentaje (%) siempre aparece en una expresión que relaciona dos cantidades. Por ejemplo: “El 13% de los niños que hacen CBTis 188 eligen el juego de Enredados para jugar después de su sesión”. En este caso, las cantidades que se están relacionando son la cantidad de niños que hacen CBTis 188 con la cantidad de esos niños que, además eligen jugar a Enredados después de su sesión.

Pero, ¿cómo podríamos calcular el número exacto de niños que eligen jugar a Enredados? Bien, es muy sencillo, pero debemos saber algunas cosas:

• Multiplicar fracciones.
• Cuántos niños hacen CBTis 188: imaginemos que fueran solo 300 niños.

¡Ya está todo listo!

Como sabemos la cantidad de referencia (el número de niños que hacen CBTis 188) solo tenemos que multiplicar la fracción que nos indica el porcentaje 13%, es decir, “13 partido de 100” por 300. Donde lo que hacemos es dividir la cantidad de referencia en 100 partes iguales y tomar 13.

Así, 300 entre 100 es 3. Que multiplicado por 13 es 39. Por tanto 39 de los 300 alumnos de CBTis 188 eligen el juego de Enredados después de sus sesiones.

VIDEOS DE APOYO

Aquí encontraras videos donde se te explica proporciones y porcentaje. 

Proporcionalidad directa

https://www.youtube.com/watch?v=nP9SwAqhVTI


Proporción inversa

https://www.youtube.com/watch?v=WzcLzSY9JLA

Porcentaje

https://www.youtube.com/watch?v=ETvdnLWIFhU

ACTIVIDAD 4:

A continuación resolverás en tu cuadernillo de Matemáticas la Sesión 4, de la página 33 a la 42.

NOTA:

Por dificultades técnicas que hay con la plataforma para recibir las actividades se realizara de la siguiente manera:

1.   Correo donde enviaran las actividades y tareas se enviaran al correo oficial: rafaelalberto.nafarrate.cb188@uemstis.sems.gob.mx.

2.   El archivo que se enviara tendrá la siguiente nomenclatura: Grupo_Actividad#_PrimerApellido_PrimerNombre.pdf, es decir, ejemplo: 1XM_Actividad1_Nafarrate_Rafael

    Este archivo debe estar en formato .pdf