CURSO PROPEDÉUTICO
Da click al grupo que te corresponda:
Reconoce el comportamiento de sucesiones aritméticas y geométricas al resolver problemas en diferentes contextos.
Sucesiones aritméticas
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden. Las aplicaciones de las sucesiones son incontables. Se utilizan abundantemente para demostrar los teoremas y las propiedades de la topología matemática, y en la muy conocida demostración del número pi.Podemos definir una sucesión aritmética de la siguiente manera.
Definición: (Sucesión Aritmética)
Es una secuencia de números, en la cual la diferencia entre dos términos consecutivos es una constante d, excepto el primer término que es dado. El valor de la constante d puede ser positivo o negativo.
Ejemplos:
La sucesión: 11 , 14 , 17 , ··· Es un ejemplo claro de una sucesión aritmética, dado que la diferencia entre dos términos consecutivos nos da una constante d de valor 3.
La sucesión: 6 , 10 , 14 , ··· Es un ejemplo claro de una sucesión aritmética, dado que la diferencia entre dos términos consecutivos nos da una constante d de valor 4.
La sucesión: 16 , 22 , 28 , ··· No es un ejemplo de una sucesión aritmética, dado que la diferencia entre el tercer y cuarto término nos da una constante d = 5 diferente al valor de la otra constante con los otros términos que es d = 6.
Cuando hablamos de sucesiones aritméticas es importante definir la notación utilizada.
| Definición: (Sucesión Aritmética) Es una secuencia de números, en la cual la diferencia entre dos términos consecutivos es una constante d, excepto el primer término que es dado. El valor de la constante d puede ser positivo o negativo. |
Ejemplos:
La sucesión:
La sucesión:
La sucesión:
Cuando hablamos de sucesiones aritméticas es importante definir la notación utilizada.
1. Concepto de sucesión
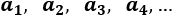
Una sucesión (o progresión) es un conjunto de números ordenados. Cada número ocupa una posición y recibe el nombre de término.
Ejemplo
Un ejemplo de sucesión es el conjunto de los números pares: 2, 4, 6, 8, 10, 12, 14,...
El término que ocupa la posición se denota por y se denomina término general o término -ésimo.
Ejemplo
En la sucesión de las pares, el primer término es y el sexto es . El término general es
En esta página trabajaremos con sucesiones con infinitos términos (no hay un último término).
2. Sucesión aritmética
Una sucesión es aritmética cuando cada término se obtiene sumando un número al término que le precede. Este número se denomina diferencia y se denota por .
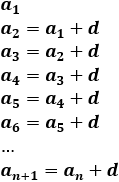
Fórmula para calcular la diferencia:
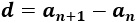
Es decir, la diferencia se obtiene restando términos consecutivos.
Si la diferencia entre dos términos consecutivos no es constante en toda la sucesión, entonces la sucesión no es aritmética.
3. Sucesión creciente y decreciente
Una sucesión es creciente cuando cada término es mayor que el anterior:
Esto ocurre cuando la diferencia es positiva: .
Una sucesión es decreciente cuando cada término es menor que el anterior:
Esto ocurre cuando la diferencia es negativa: .
Nota: si la diferencia es , la sucesión es constante (todos los términos son iguales).
Sucesiones geométricas
Las series geométricas tienen muchas aplicaciones importantes.
Podemos definir una sucesión geométrica de la siguiente manera.
| Definición: (Sucesión Geométrica) Una sucesión geométrica es aquélla en la cual el cociente entre dos términos consecutivos es una constante llamada razón r y puede ser positiva o negativa. |
Por ejemplo:
Sea la sucesión 5, 15, 45, 135, 405, 1215, ... es geométrica porque cada término es multiplicado por la misma contante, que es 3.
Sea la sucesión 3, 9, 27, 81, 243, 729, ... es geométrica porque cada término es multiplicado por la misma contante, que es 3.
Sea la sucesión -2, 4, -8, 16, -32, 64, ... es geométrica porque cada término es multiplicado por la misma contante, que es -2.
Cuando hablamos de sucesiones es importante definir la notación utilizada.
| Notación: (Sucesión Geométrica) Comunmente se denominan los términos de una sucesión de la siguiente manera: a(2) = segundo término de la sucesión a(n) = n-ésimo término de la sucesión r = razón común |
1. Concepto de sucesión geométrica
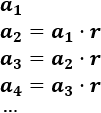
Una sucesión geométrica (o progresión geométrica) es una sucesión en la que cada término se obtiene multiplicando al término anterior por un número llamado razón.
La razón de una sucesión geométrica se denota por y debe ser constante en toda la sucesión.
2. Razón de una progresión
La razón de una progresión geométrica se calcula dividiendo términos consecutivos:
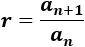
La razón de una progresión geométrica se calcula dividiendo términos consecutivos:
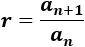
3. Término general
El término general de una sucesión geométrica se calcula a partir del primer término y de la razón :
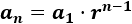
El término general permite calcular cualquier término de la sucesión sin necesidad de calcular los anteriores.
El término general de una sucesión geométrica se calcula a partir del primer término y de la razón :
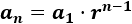
El término general permite calcular cualquier término de la sucesión sin necesidad de calcular los anteriores.
4. Monotonía de una progresión
La monotonía de una sucesión geométrica depende del signo del primer término y del valor de la razón:
Si el primer término de la sucesión es positivo, entonces
si , la sucesión es creciente
si , la sucesión es decreciente
Si el primer término de la sucesión es negativo, entonces
si , la sucesión es decreciente
si , la sucesión es decreciente
En cualquier caso, si , la sucesión es constante; y si , es alternada.
Las progresiones alternadas son aquellas en las que cada término tiene el signo contrario al del término que le precede.
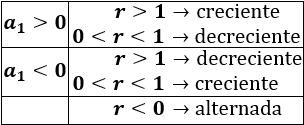
La monotonía de una sucesión geométrica depende del signo del primer término y del valor de la razón:
Si el primer término de la sucesión es positivo, entonces
si , la sucesión es creciente
si , la sucesión es decreciente
Si el primer término de la sucesión es negativo, entonces
si , la sucesión es decreciente
si , la sucesión es decreciente
En cualquier caso, si , la sucesión es constante; y si , es alternada.
Las progresiones alternadas son aquellas en las que cada término tiene el signo contrario al del término que le precede.

5. Suma de términos
Para sumar los primeros términos de una progresión geométrica disponemos de varias fórmulas:
Primera fórmula:
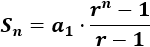
Segunda fórmula:
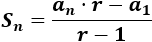
Nota: la segunda fórmula se ha calculado utilizando la fórmula del término general en la primera fórmula de la suma.
Nosotros utilizaremos la primera en los problemas.
Para sumar los primeros términos de una progresión geométrica disponemos de varias fórmulas:
Primera fórmula:
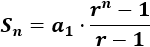
Segunda fórmula:
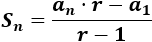
Nota: la segunda fórmula se ha calculado utilizando la fórmula del término general en la primera fórmula de la suma.
Nosotros utilizaremos la primera en los problemas.
6. Suma de todos los términos
Cuando la razón de la progresión es se pueden sumar todos los términos mediante la fórmula
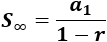
VIDEOS DE APOYO
Aquí encontraras videos donde se te explica cada una de las asociaciones aritmética y geométrica.
Sucesiones Aritméticas
https://www.youtube.com/watch?v=FGoSqeFl5zg
Sucesiones Geométricas
https://www.youtube.com/watch?v=qUEeAVqCpXY
ACTIVIDAD 3:
A continuación resolverás en tu cuadernillo de Matemáticas la Sesión 3, de la página 25 a la 32.
Link para enviar actividad: Dar click aquí
Fecha Limite de entrega Martes 29/10/2020 11:00am
Cuando la razón de la progresión es se pueden sumar todos los términos mediante la fórmula
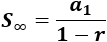
VIDEOS DE APOYO
Aquí encontraras videos donde se te explica cada una de las asociaciones aritmética y geométrica.Sucesiones Aritméticas
https://www.youtube.com/watch?v=FGoSqeFl5zg
Sucesiones Geométricas
https://www.youtube.com/watch?v=qUEeAVqCpXY
A continuación resolverás en tu cuadernillo de Matemáticas la Sesión 3, de la página 25 a la 32.
Link para enviar actividad: Dar click aquí
Fecha Limite de entrega Martes 29/10/2020 11:00am




No hay comentarios:
Publicar un comentario