Álgebra Parcial 3: Ecuación Lineal
Da click al grupo que te corresponda:
Ecuaciones lineales
En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, análisis estructural, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Las ecuaciones de la forma ax + b = 0 son muy sencillas de resolver, basta con despejar la x.
Despejar la x significa dejar la x sola a un lado del signo igual. Para pasar un número, o una variable, al otro lado del signo igual tenemos que seguir estas reglas:
- Si está sumando pasa restando y si esta restando pasa sumando. En nuestro caso quedaría ax = -b
- Si está multiplicando pasa dividiendo y si está dividiendo pasa multiplicando. En nuestro caso x = -b/a.
Una forma más sencilla de ver este método de despejar, es que a los dos miembros de las ecuaciones se les realizan exactamente las mismas operaciones a cada uno.
Como son iguales, el uno y el otro, al realizarles exactamente la misma operación su resultado variara exactamente de la misma manera (en el caso que sea cero un multiplicando o un dividendo esta regla no se aplica).
Pasos:
- Se efectúan las operaciones indicadas de cada miembro, si las hay.
- Se añaden los mismos términos a cada lado del igual a fin de dejar todas las expresiones con incógnita de un lado de la ecuación y todas las cantidades conocidas del otro lado.
- Se reducen los términos semejantes.
- Se despeja la incógnita dividiendo entre el coeficiente de la incógnita ambos miembros de la ecuación.
- Se comprueba que el resultado obtenido sea correcto reemplazándolo en la ecuación original.
Ejemplo explicativo:
Existen muchas ecuaciones que a simple vista se puede suponer que son de un grado superior pero que fácilmente se convierten en ecuaciones de 1er grado al factorizar ó añadir términos para desaparecer los términos de grado superior a uno.
Ejemplo explicativo:
Ejemplos:
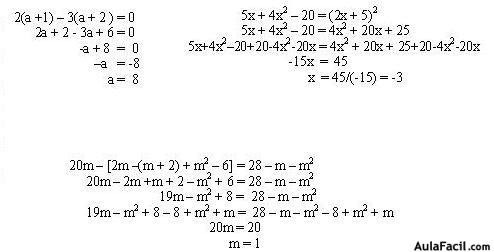
Actividad No. 1
A continuación darás click en cada uno de siguientes link que te mostrara los temas en video y realizaras en tu cuaderno cada uno de los ejercicios de los siguientes videos.
ECUACIONES DE PRIMER GRADO Ó LINEALES
Videos
Es ejemplo: 1ZM_Actividad1_Ponce_Juan
"NO PONER MIS DATOS, SON LOS DE USTEDES"
Este archivo debe estar en formato .pdf y fecha limite de entrega Domingo 29/11/2020 11:59 pm.



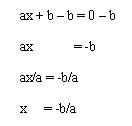

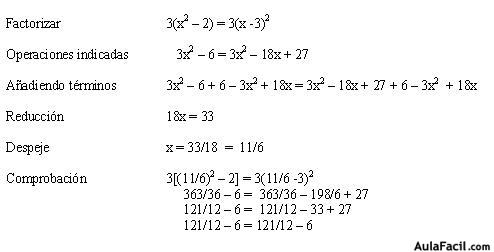


Maestro lo mandamos en diferentes pdfo en uno solo
ResponderEliminar